本文首先介绍DRAM的通用微架构、工作机制、各级功能、数据总线结构以及HBM3的基本知识。然后分析DRAM的RAS需求,包括DRAM故障错误定义及分类,阐述故障隔离的必要性以及DRAM的RAS特性。最后,补充关于有限域和中国剩余定理的数学基础,并扩展介绍用于DRAM的线性分组码和Chipkill ECC技术。
1 DRAM基础介绍
虽然DRAM位单元的基本结构和操作相当简单,但单颗DRAM芯片包含数十亿个这样的位单元。一个复杂的架构已经在许多代DRAM设备上延续发展,能够实现非常大的容量,同时最大限度地降低成本。由于HBM3中的每层DRAM芯片在内部架构上与其他当代DRAM设备(例如GDDR6和DDR5)非常相似,因此下面的讨论和技术通常也适用于这些DRAM变体。在本节中,首先介绍DRAM的微架构和存取机制,理解数据总线的构成和读写时序的标准,再对HBM3做基本介绍。
1.1 DRAM微架构
1.1.1 DRAM位单元
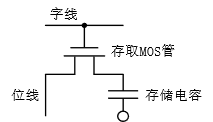
DRAM的工作原理是将信息作为电荷存储在电容中。图1为DRAM位单元的原理图,主要由字线(Wordline)、位线(Bitline)、存取MOS(Metal Oxide Semiconductor)管和存储电容组成。写入数据的方法是将位线驱动到低电压或高电压,并激活字线以打开存取MOS管。接着,存储电容根据位线的状态充电或放电。最后,字线电位置低,存取MOS管关闭,该存储电容将保留所写入的值。为了读取存储的数据,位线被预充到一个中间值,然后字线被激活。如果存储电容被充电,会导致位线上的电压增加;如果存储电容被放电,位线上电压将下降。
1.1.2 DRAM MAT
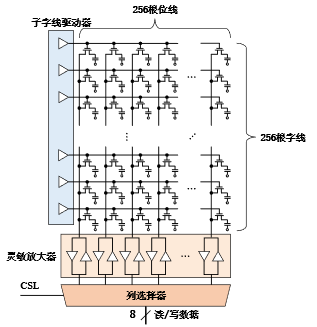
基于上文的位单元构建MAT(Memory Array Tile)结构,如图2所示。这可以看作由若干字线、位线和存储单元组成的二维阵列,字线和位线分别代表MAT的行和列,一定数量的字线和位线形成了MAT的宽度和高度。考虑到成本,MAT应该尽可能大,以最小化与每个MAT的外围逻辑电路相关的区域开销。同时,MAT的大小受字线和位线上电容的限制。
1.1.3 子阵列
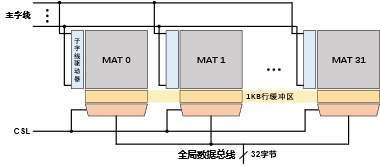
DRAM在存储阵列方面采用分层结构,而MAT是存储阵列的最小组成单元。由于限制MAT尺寸的因素之一是字线的长度,因此一种称为子阵列的结构将许多块MAT连接在一起,构成了支持长字线的结构,同时也形成了比单个MAT更大的存储阵列。图3显示了通用的子阵列设计。从图中可以看到,32块MAT被平铺成一排,使用一组公共的主字线拼接在一起,这使得每块MAT中对应的子字线可以由子字线驱动器驱动。由于每个MAT有一个选择8位数据的列选择器,本文采用的子阵列将256 bit×32=8192 bit=1KB锁存到它的灵敏放大器组(又称行缓冲区)中。从这1KB的标准数据中,行缓冲区可以同时从每块MAT中选择8位,共32字节数据进行传输。因此,子阵列构型对给定DRAM访问的可用带宽有直接影响。
1.1.4 DRAM Bank
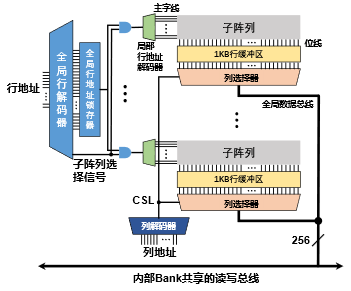
DRAM的Bank是向内存控制器公开的最底层单元。HBM3规定每层DRAM芯片有128个Bank。事实上,一个Bank由几十个子阵列组成。图4显示了Bank的逻辑结构,主要包含子阵列模块、局部行地址解码器、列解码器、全局行地址锁存器、全局行解码器以及内部多Bank共享的读写总线。通过激活其中子阵列中的一条字线,可以选择Bank中的某一行。Bank中的行解码器通常是多级的:预解码器首先将部分解码的行地址发送到每个子阵列,子阵列选择信号输入到局部行地址解码器进行最终解码。
1.1.5 DRAM Bank Group
由于对更高带宽DRAM设备的需求不断提高,DRAM接口的数据速率一直在提高。然而,CSL和数据总线的高电容和线上过重的负载是限制DRAM内部数据路径传输频率的主要因素。因此,在I/O总线上传输数据的时间已经小于对单个DRAM的Bank连续读或写请求之间的最小时间,从而限制了DRAM接口处数据速率的提升。
为了解决DRAM接口数据速率与DRAM的Bank连续读/写速率不匹配问题,从DDR4、GDDR5和HBM等内存标准就开始支持Bank Group结构。在给定DRAM通道中的Bank被划分为几个Bank Group,通常每个Bank Group包含4个Bank,如图5所示。对不同Bank Group的访问命令可以紧密地连续下达,而不考虑单个Bank的操作周期。连续读/写的列命令到不同Bank Group之间的较短延迟定义为计时参数tCCDS;向同一Bank Group连续发出读/写命令的时间间隔是较长的计时参数tCCDL。
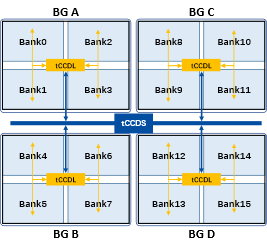
图6展示了HBM中同一Bank Group和不同Bank Group的读操作。对不同Bank Group下达的连续读命令可以用tCCDS = 2nCK间隔,而对同一Bank Group下达的连续读命令之间须以tCCDL = 4nCK间隔。为了有效地利用DRAM全部带宽,内存控制器必须在不同的Bank Group之间交替请求访问,以确保其连续访问的数据在总线上进行无缝传输。
1.1.6 通道
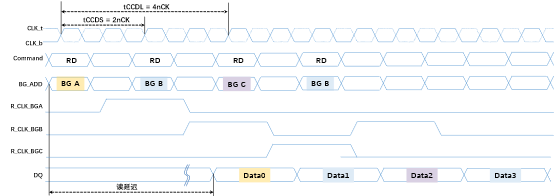
类似地,根据DRAM标准,多颗芯片可以与内存控制器组合形成一个接口,被称为通道。移动设备的DRAM(比如LPDDR系列)一般每个通道使用一颗DRAM芯片,而桌面设备的DRAM(比如DDR系列)通常聚合4-16个DRAM芯片以形成连接到通道的排(Rank)。一般来说,最多8排可以对同一通道进行分时复用。图7展示了一个典型的双排DDR4系统,每排有四颗DRAM芯片。 同时,该图也展示了每颗芯片如何提供一个16位的接口,使得该接口与本排中所有其他芯片连接形成一个64位排接口。这两个64位排接口然后通过通道的分时复用与内存控制器通信。注意,除了64位数据外,DRAM通道还向每个芯片传输命令和地址信息(为简单起见,没有说明)
HBM3标准沿用HBM2和HBM2E标准中的伪通道结构。命令接口由两个伪通道共享。每个通道中的两个伪通道都是半独立运行的:它们共享通道的行、列命令总线以及时钟总线,但是分别执行行、列地址解码以及命令。两个伪通道都有足够的命令带宽来充分利用各自的数据总线。因此,在本文的其余部分中,常规DRAM通道和HBM3伪通道之间几乎没有区别。
1.2 HBM3基本介绍
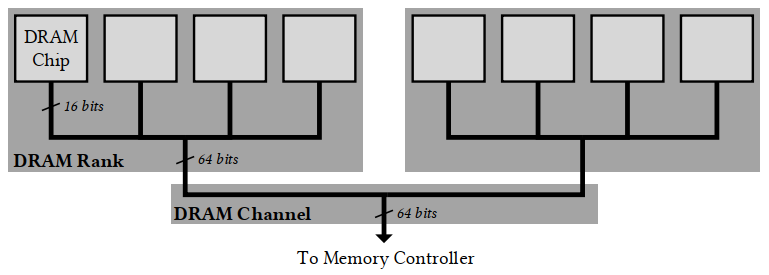
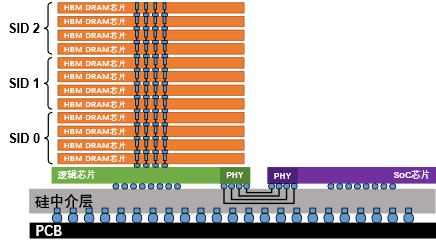
图8展示了高带宽存储器HBM3的3D堆叠结构,由12个DRAM芯片和一个底层逻辑芯片组成。每个DRAM芯片有4个通道,而16个通道由一个标准的四层堆叠芯片组成,该四层堆叠由一个堆叠标识(Stack-ID,SID)识别。每个伪通道有16个Bank,每个Bank逻辑上有一块位宽为1KB的行缓冲区。16个Bank被组织成4个Bank Group。数据和地址接口的I/O驱动电路位于逻辑芯片上。每个通道都有一组TSV,将逻辑芯片上相关的I/O驱动器与其上方堆叠的DRAM芯片的通道连接起来。HBM3通过硅中介层上的细间距互连技术(PHY)连接到主处理器。
由于HBM具备大容量和高带宽的优势,其近年来一直是最具发展前景的存储技术,人工智能和数据中心市场的快速增长将推动HBM的不断改进。表1展示了HBM1、HBM2、HBM2E和HBM3的产品设计特性总结。可以看到,HBM存储容量不断提升,而且由于引脚数据速率的提高,HBM3的带宽也有明显提升。
| HBM1 | HBM2 | HBM2E | HBM3 | |
|---|---|---|---|---|
| 数据速率 | 1.0Gb/s/pin | 2.4Gb/s/pin | 5.0Gb/s/pin | 8.0Gb/s/pin |
| 带宽 | 128GB/s | 307-346GB/s | 512-640GB/s | 896-1024GB/s |
| 存储密度 | 1GB | 2/4/8GB(2/4/8层) | 8/16GB(4/8层) | 16/24GB(8/12层) |
| 通道 | 8CH | 8CH, 16pCH | 8CH, 16pCH | 16CH, 32pCH |
| I/O数量 | 256IO/CH | 128IO/CH | 64IO/pCH | 32IO/pCH |
| 突发长度 | 2/4 | 2/4 | 4 | 8 |
| 电源电压 | VDDC/Q=1.2V,VPPE=2.5V | VDDC/Q=1.2V,VPPE=2.5V | VDDC/Q=1.2V,VPPE=2.5V | VDDC/Q=1.1V,VPPE=1.8V |
2 DRAM的RAS需求
互联网信息的爆炸式增长以及随之而来的数据存储和计算需求,导致在非常大规模的数据中心内需要部署异构且复杂的解决方案。这些庞大的架构占满了服务器、存储和网络硬件,以“Lights-out”方式运行,这就使RAS的三个方面成为了焦点。首先,随着存储或传输的组件和比特的总量不断增加,即使传统上不常见的错误也开始变得普遍。任何由材料退化、环境影响或制造缺陷引起的极端情况都可能影响系统的可用性或性能。其次,错误检测和纠正必须完全自动化,并尽量减少人工交互。由于需要更换硬件的修复事件数量应该保持在绝对的最小值,因此有必要清楚和明确地识别出故障组件,并尽量减少在修复上花费的时间。此外,虽然持久或永久性错误的处理很容易自动化,但间歇或短暂故障也可能频繁出现,并有可能对应用程序性能、正常运行时间和用户体验产生负面影响。因此,DRAM的设计需要尽量减少RAS机制引起的干扰,并提供确定性行为。
2.1 DRAM故障错误
由于DRAM自身的复杂性,DRAM易受到各种故障的影响。本节将对DRAM中比较常见的故障类型进行介绍,主要包括DRAM位单元的固有故障、间歇性固有故障以及数据信号传输过程中的故障。
1. 位单元固有故障
随着DRAM工艺技术的持续收缩,DRAM存储阵列中的固有故障数量也在增加,导致越来越多的位单元无法正常运行。继续收缩尺寸已经很小的DRAM存储单元阵列会增加生产制造故障的发生率,主要原因有两点:(1)长宽比增加使得维持正确存取操作所需的电荷更加困难;(2)存储单元间距变窄会导致更多的干扰误差。行业研究表明,制程小于等于20nm的DRAM技术中固有故障的误码率可能已经在$10^{-4}-10^{-6}$之内。此外,即使假设所有固有的错误都是永久性的,并且可以在DRAM生产测试期间被识别出来,使用DRAM中预先留置的行、列冗余修复不断增加的固有错误单元需要很大的代价。例如,如果通过冗余修复方案处理固有故障,那么当固有故障发生率从$10^{-7}$增加到$10^{-6}$时,面积开销预计会从<10%激增到40%左右。
2. 位单元间歇性固有故障
虽然固有故障的具体细节是DRAM制造商的机密信息,但有研究表明,对于可变保留时间(Variable Retention Time, VRT),固有故障可能表现为随机误码。每个DRAM位单元电容都会随着时间漏电,因此所有位单元必须定期刷新充电。部分位单元在固定的刷新间隔内偶尔漏电过快,产生保留错误。这些间歇性的固有故障随机且不频繁地产生错误,因此在制造的测试阶段不容易检测到。如果故障在导致错误之前没有被识别出来,那么行/列冗余就会失效。由VRT引起的保留错误已经是随机DRAM错误的一个主要来源,预计在工艺收缩的DRAM产品迭代中会增加。如果未来DRAM工艺的收缩趋势加剧了VRT,并导致更频繁的间歇性固有故障,可以预见的是,它们对DRAM可靠性的影响将比其增加的误码率所表现的更加严重。
3. 信号传输路径故障
DRAM的故障位置除了存储阵列外,信号的传输路径故障也是数据错误的一个主要来源。表2列举出了DRAM信号传输路径的常见故障类型、原因以及对信号完整性的影响。
| 传输故障 | 描述/原因 | 对信号完整性的影响 |
|---|---|---|
| 介电损耗 | 信号衰减与迹长、频率相关 | 所有数据位都会受到影响,导致信号衰减 |
| 趋肤效应 | 导体电阻随频率的变化不均匀 | 同上 |
| 电磁干扰/串扰 | 紧密排列线路的电磁/电容耦合 | 在同一时间点,可能只有少数总线线路/通道受到影响 |
| 信号偏移 | 路径长度变化导致时序变化 | 随机影响 |
| 信号抖动 | 给定信号的连续周期之间的电压、温度和串扰的波动会影响信号的传播时间 | 难以建模和描述 |
| 码间干扰 | 一条导线上过去的信号对同一导线的后续信号有残余影响 | 受影响的位线数量随机,影响其他数据信号 |
| 同时切换输出 | 当一个总线通路上的许多信号同时切换时,它们会引起其他信号的耦合 | 影响其他数据信号 |
这些故障主要由以下两个因素导致:
(1)DRAM的设计和制造过程中出现的问题。设计错误、制造工艺不当或材料质量不佳等因素引起了技术方面故障。例如,由于设计存在问题,DRAM中的某些控制电路可能会出现故障或差错,从而导致DRAM无法正常工作。此外,由于制造工艺不当,比如3D堆叠HBM层与层连接的TSV因技术加工问题存在故障风险,可能导致DRAM无法正常传输信号。 (2)DRAM的外部环境变化影响。温度变化、湿度变化、电磁干扰等外界因素可能导致DRAM的失效。例如,由于外界温度变化或者自身散热问题,DRAM中的电路和组件会受到影响,从而导致DRAM性能下降,无法正常工作。另外,由于太阳风暴、宇宙射线的电磁干扰或者粒子扰动,DRAM出现耦合串扰、信号抖动等情况的概率增大。
2.2 故障隔离
DRAM故障隔离是对DRAM存储阵列中各种故障引起的错误的一种管理机制,这些故障被隔离在一定的边界内,而无需考虑OD-ECC如何操作。根据ECC符号大小选择故障隔离界限,最大限度地提高多比特故障的校正能力。设计必须尽可能保证最常见的多比特故障模式产生的是被限制在可纠正的符号尺寸内的错误。表3列举了部分可隔离故障和不可隔离故障的不同故障模式,以及故障隔离界限的划分对HBM3的OD-ECC设计的影响,若OD-ECC可以尽可能多地检测并纠正故障隔离界限内的错误,那么SDC事件发生的概率将会随之降低,从而增强HBM3的RAS特性。

2.3 DRAM的RAS特性
可靠性是DRAM提供正确服务的能力。设计一个可靠内存系统的一种方法是能够检测和纠正可能导致错误的故障。这种设计的典型例子就是使用OD-ECC来检测DRAM中特定位置的故障,并将存储于该位置的数据在被处理器接收之前进行纠正。
可用性是DRAM在能力或性能可能下降的情况下随时准备提供正确服务的能力。获得可用性的一种方法是使数据从错误中恢复,这样服务就不会因为错误而中断。对于DRAM的OD-ECC而言,如果其检测到错误,但无法纠正,则可以报告内存控制器使DRAM特定地址的物理页面引退,以便将来不向该位置分配数据。如果恢复不成功,系统崩溃并重置,那么这将导致一段时间的停机,这意味着在这种停机时间内系统不可用。量化可用性的一种方法是判断“9的数量”。例如,5个9的可用性意味着系统在99.999%的时间内处于运行状态,即在一年的系统运行中大约有5.25分钟的停机时间。
可服务性是系统诊断和修复DRAM中可能导致(或已经导致)错误的故障的能力。例如,内存修复技术允许具有不可纠正的永久故障的内存位置通过替换为备用内存来进行物理修复,这将提供可服务性。可服务性可能是“在线”状态,即系统继续可用;也可能是“离线”状态,即系统在被服务时不可用。
3 相关纠错码
3.1 线性分组码
DRAM中OD-ECC通常采用线性分组码来最小化解码延迟,例如SEC码、SEC-DED码和RS码。当内存控制器向DRAM写入数据时,线性分组码使用数据的线性组合产生冗余校验位,而数据和校验位的有效对被称为码字。一个$(n, k)$线性分组码从k位数据(记为$m$)生成一个$n$位码字(记为$c$),可以用$k×n$生成矩阵(记为G)来描述:
\[c=mG\tag{1}\]在读取DRAM中数据时,OD-ECC接收到的码字(记为$c_e$)可能有一个错误(记为$e$),写为
\[c_e=c+e\tag{2}\]线性分组码通过与转置校验矩阵(记为H$^T$)相乘来解码一串码字
\[S=c_eH^T\tag{3}\]H矩阵的维数为$(n−k)×n$,在公式(3)中有$n−k$位输出。该输出称为校正子,表示为$S$。如果G和H矩阵满足公式
\[GH^T=0\tag{4}\]则校正子遵循
\[S=(c+e)H^T=mGH^T+eH^T=eH^T\tag{5}\]并且对于所有正确码字,$S$必须为零,即$e=0$。而具有非零校正子的码字,仅由错误决定,无论受保护的数据如何。 如果H矩阵为每一类错误生成唯一的非零校正子,则OD-ECC可以识别每一类错误。识别后,OD-ECC通过翻转受影响错误位置的比特(或多比特纠错情况下的所有错误比特)来恢复数据。例如,SEC码的H矩阵应具有唯一的非零列值。对于单比特错误,公式(5)计算的校正子与某一列值相同。如果每列都是唯一的,OD-ECC可以识别到错误并通过翻转该列位置上的比特来纠正它。如果一串码字有多个错误位
\[c_e=c+e_1+e_2+\dots+e_m\tag{6}\]则输出校正子是各个校正子的总和
\[S=c_eH^T=e_1H^T+e_2H^T+\dots+e_mH^T\tag{7}\]3.2 Chipkill ECC
在DRAM设备中,大多数故障引起的错误表现为单比特错误,但大型系统(例如数据中心和超级计算机)需要比SEC ECC更高的可靠性来保证整体性能和RAS指标。这种对DRAM更强保护的需求推动了专用于大规模系统中DRAM保护的标准Chipkill ECC。即使DRAM Rank层级的任意单颗DRAM芯片出现故障,启用Chipkill ECC的系统也可以正确运行。
Chipkill ECC实际上还包含SSC-DSD。在有限域表示下,它是GF$(2^q)$上汉明距离为4的线性分组码,比SDDC的汉明距离大1,增加了完全检测双符号错误的能力。它也可以用校验矩阵H来定义,其中矩阵和向量的分量被认为是GF$(2^q)$的元素。设$h_i(0 \leq i < 2+2^q)$是H矩阵的列向量。SSC-DSD必须满足以下条件:
(1)$h_i \neq X \cdot h_j, X \in GF(2^q)$
(2)$h_i + X_1 \cdot h_j \neq X_2 \cdot h_f, i \neq j \neq f, 且X_1, X_2 \in GF(2^q)$
假设$r$为GF$(2^q)$上SSC-DSD的校验符号数量。例如,对于$r=3$,长度为$N<2+2^q$ 符号的码字可以通过GF$(2^q)$中元素来构造。码字的校验矩阵表示为
\[H=\left[ \begin{matrix} I & I & I & \cdots & I & I & O & O\\ I & T & T^2 & \cdots & T^{N-4} & O & I & O\\ I & T^2 & T^4 & \cdots & T^{2(N-4)} & O & O & I \end{matrix} \right] \tag{8}\]其中$I$是$q×q$的单位矩阵,$O$是$q×q$的零矩阵,$T$是$q×q$的$X$的伴随矩阵。如果$X$是伽罗华域中的本原多项式$p\left(x\right)=a_0+a_1x+a_2x^2+\cdots+a_{q-1}x^{q-1}$的一个根,则$X$的伴随矩阵为
\[T=\left[ \begin{matrix}0&0&\cdots&0&a_0\\ 1&0&\cdots&0&a_1\\ 0&1&\cdots&0&a_2\\ \vdots&\vdots&\ddots&\vdots&\vdots\\ 0&0&\cdots&1&a_{q-1}\\ \end{matrix} \right]\]接下来,利用公式(8)的校验矩阵H。H矩阵的最后三个列位置为校验符号的位置,H矩阵的其他列位置可以指定为数据符号的位置。校验符号可以用异或树生成,异或树也同样可以产生校正子向量$S=(S0,S1,S2)$。每个校正子分量$S_i$为$q$位,表示公式(8)第i行奇偶校验的结果。由公式(8)可知,假设$E$是数据符号位置$i$处的单符号错误,则$E$是以下三个方程的唯一解:
\[\begin{cases} S_0 = E^{'} \\ S_1 = T^iE^{'} \\ S_2 = T^{2i}E^{'} \end{cases}\tag{9}\]如果$E$是校验符号位置$i$上的错误,其中$i=0、1或2$,并且其他两个校正子分量为零,则只需要将第$i$行前$N-3$列奇偶校验结果赋给该校验符号即可实现纠正。以下步骤可以用于查找可纠正的单符号错误,并能检测出不可纠正的多符号错误。
(1)如果向量$S$是零向量,则没有错误。如果$S$不为零,执行步骤(2);
(2)如果其中一个校正子分量$S_i \neq 0$,而其他两个校正子分量为零,则说明第$i$行的校验符号出错。否则,执行步骤(3);
(3)如果公式(9)有唯一非零解,则可以确定数据符号出错的位置;如果没有,则检测到不可纠正的错误。