全息存储的基础知识

2023-09-08
于勤 (Qin Yu)
全息存储
resource

本文档的主要内容包括全息存储的基础知识以及目前本课题组在全息存储的纠错码方向的研究成果总结。

全息存储的基础知识

随着大数据，物联网和人工智能等新一代信息技术的快速发展，全球产生的数据量数据呈爆炸式增长的趋势。根据IDC预测，至2025年，全球产生的数据量将达到175ZB[1]。自从“新基建”提出以后，5G、大数据中心、人工智能、工业互联网等正加速推进，数据成为新基建的基础元素。数据就是财富，原始数据不可再生。大数据科学更依赖于全局数据，越大、越繁杂的数据全集是各种相关性分析和知识挖掘的基石，海量数据的低成本和超长期保存已成为目前网络信息产业领域的重大需求[2]。在海量数据中，并非所有的数据都会被频繁访问。根据访问频率由高至低，可以将数据分为热数据、温数据和冷数据。在大数据时代，80%的数据最终会变为不被频繁访问的冷数据。研究如何长期安全节能地保存温冷数据，是目前存储行业面临的一个难题。

以闪存等为代表的固态存储技术虽然具有广泛的应用扩展空间，但是也面临存储密度（550 Gb/in2）受限的问题，而且这种技术还存在擦写次数有限和电荷流失等缺点，不适合冷数据的低成本长期保存。当前数据中心存储数据的主流介质还是磁盘和磁带之类的基于磁技术的存储机制，存在寿命有限的问题（磁盘5年，磁带10年），而且已经趋近于存储密度（735 Gb/in2）的理论极限[3][4][5]。随着存储数据量的需求不断增长，数据中心的能耗也随之大幅度增加。在Google公司的数据中心，其能耗费用已经超过了其维持管理费用的50%。因此，降低存储数据的能耗也已经成为大型数据中心经营管理的主要目标之一。

与其他存储方式相比，光存储具有节能、长期保存以及成本低廉等优点，适合温冷数据存储。目前最为常见的光存储技术就是光盘，如果用波长为λ的光作为数据存储的光源，则其理论存储面密度约为1/λ2。 从最早的 CD，到 VCD、DVD 再到现在的蓝光 BD 光 盘，光盘存储的密度也在不断增大。然而目前的光盘存储仍是按位存储的二维面存储(尽管有的光盘可以实现多层存储，但层数有限)，而且增大了伺服控制的难度，每一个记录位都只表示 0 或 1 的状态，其存储密度受记录位的尺寸的限制，记录位的尺寸越小则数据存储密度越大。

全息光存储是一种以二维数据页为读写单位的三维体存储技术，突破了传统光盘二维点阵排列的局限，极大地提高了光存储的存储密度，数据转换速率以及存储容量[6-11]。光全息存储最大的特点是突破了传统光盘存储的二维面存储模式，采用三维体存储模式，其理论存储密度为 1/λ3。由于存储密度提升了一个维度，因此可以将现有的光存储密度提升几个数量级[12-14]。多维度光存储、超分辨近场光存储，全息存储等新型存储技术将在未来极大地满足人类的生产生活需要，其中光全息存储将在海量冷数据存储中占有极大优势。

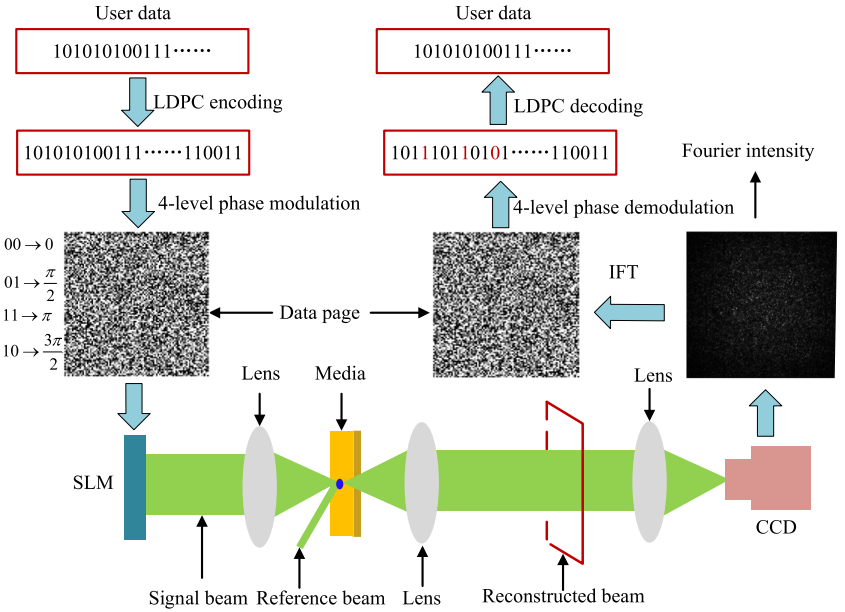
相位型全息存储系统的记录，读取和相位恢复过程

图1 相位型全息存储系统的记录，读取和相位恢复过程

光全息数据存储利用全息拍照原理，将物的振幅和相位信息以全息图的形式记录在全息材料中。如图 2所示，在记录过程中，光经过空间光调制器(一种二维光学元件，可以显示想要上载的二维图 案)，携带上二维图案的信息称之为物光。物光与另一束已知光场的光(参考光)在全息材料中进行干涉，形成复杂的光场分布，全息材料对不同强度的光场进行相应的响应，产生材料的变化并最终形成某种稳定结构，称之为全息图。这样就将物光信息记录在了全息材料中。在读取过程中，只需要利用同一束参考光以与记录时同状态的方式照射材料中的全息图，就会通过全息图的结构对参考光的耦合作用，将光能耦合到物光光场中，发生光的衍射。衍射出的光又称为重建光，重建光实际上与原始物光场的分布是一致的，因此就读出了物光信息。重建数据页大概出现在图1中的红色虚线处。然而，目前的传感器如CCD 或 CMOS 等只能直接探测光的强度，因此相位信息是无法被直接得知的，必须通过一定的方法将相位分布转化成为强度分布，再用CCD或CMOS进行探测[15]。因此，在重建光后面放置一个傅里叶变换透镜，使重建光位于傅里叶变换透镜的前焦面，再将CCD放置在傅里叶变换透镜的后焦面上，重建光的相位分布经过傅里叶变换后的强度分布被CCD探测到。CCD捕捉的傅里叶强度信息用于恢复相位信息。

根据参考光路与信息光路是否同轴，可以将全息存储系统划分为同轴式系统和离轴式系统。离轴参考光路相对比较复杂。常采用角度复用，该方式会造成记录材料的部分浪费，而且每次角度控 制后都需要静止一段时间，因此属于静态读写。同轴式系统通常采用位移复用，造成更少的记录材料浪费，而且记录过程中材料一直在运动，属于动态读写。结构简单紧凑、操作简单、兼容性强等特点将成为全息存储技术进一步实用化和产品化重要方向。本研究也是围绕相位型同轴全息存储系统进行开展的。

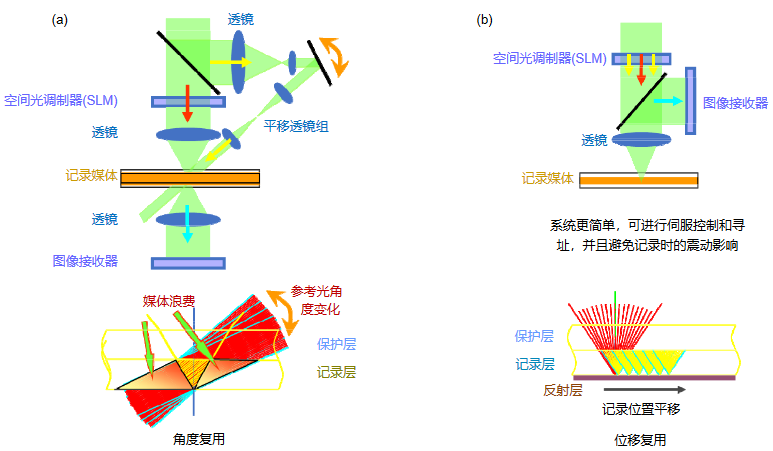
离轴全息存储（a）和同轴全息存储(b)系统对比图

图2 离轴全息存储（a）和同轴全息存储(b)系统对比图

根据编码方式的不同，全息存储系统被划分为振幅型全息存储、相位型全息存储以及复振幅型全息存储系统。振幅型全息存储是传统全息存储技术，有两大缺点；首先，振幅编码的编码率相对较低，从目前采用的方法来看，振幅编码的编码率最大是1，但是由于过多的像素使用将带来更大的误码率和材料消耗，因此一些经典的振幅编码，如3：16 编码(即16个编码像素作为一个单元，一个单元内只有3个像素是亮的，其余像素是暗的)通过3个亮像素的不同位置组合可以在一个单元内存储 8 bit 信息，其编码率为0.5。其次，记录材料往往是放在记录物镜的后焦面附近，以提高记录密度，但是振幅编码在经过物镜聚焦后，其中心强度在后焦面上过于集中，会导致超出材料的动态响应范围而产生强度响应饱和现象，不仅使信噪比变低，而且消耗材料也 更多，无法在同一位置附近复用更多的全息图。为了解决振幅调制出现的能量过于集中的问题，一种方法是将记录材料离焦的方法，但该方法会导致记录密度降低。另一种方法是将相位调制加入到振幅调制中，通常是在振幅调制后加入一个随机相位板，可以使材料中的能量从中心集中状态变为均匀分布状态， 大大提高了信噪比，即提高了存储密度。但是这仍然无法解决振幅编码率低的问题，而且虽然在全息存储系统中用到了相位调制，但是相位信息具体是什么并没有去探测。

相位作为信息编码比振幅编码具有更大的优势。因为相位编码本身就是相位调制，不需要再加入随机相位板，这样系统更简单，也具有很高的信噪比。相位编 码的编码率比振幅编码的编码率大幅提高，其编码率 可以很容易突破 1 的限制。从实现方式上看，利用相位进行编码也比以前更加容易。在硬件方面，自2000年以来，纯相位的空间光调制器件发展很快，液晶型的空间光调制器刷新速度不断加快，像素尺寸不断减小，而且相位调制深度不断加大。这就为相位编码提供了很好的支撑。与传统的振幅编码相比，一个4阶相位编码的编码率可以达到振幅编码的4倍，8阶相位编码的编码率可以达到振幅编码的6倍。因此，相位编码可以进一步提高全息存储的存储密度和数据转换速率。相位型同轴全息存储系统是全息存储实用化和商品化的重要方向。

当前全息技术要面对的最大挑战是信号的干扰问题。由于全息采用的是用激光曝光光盘上的图像，通过干涉原理进行记录，衍射原理进行读取，然后用探测器捕捉的重建光强度信息进行解码。这样的工作原理导致全息驱动器对于光的干涉和其他噪音的干扰非常敏感。现阶段，不得不通过更为复杂的纠错和调制方式来保证数据的准确性,这样带来的弊端就是全息存储驱动器的读写速度无法提升[15-20]。

目前，已有很多工作致力于解决全息存储可靠性的问题。通过沿剪切方向对每个像素的相位进行预积分来修改输入信号，以消除慢变相位误差，并在出现光盘位移相位误差时减少解码误差[21]。Zhao等[22]提出了一种基于相位分布特征的相位决策方法，自适应匹配每个相位数据页的相位阈值。为了消除错误率，Xu等[23]在解码过程中使用了不等间距的四级相位对编码来防止误读，但牺牲了数据页中数据像素数的一半。 Lin等[24]提出了一种基于IFT算法的以嵌入数据为先验信息的单次非干涉式迭代相位检索方法，利用已知的先验相位数据可以实现准确、快速的相位检索。Hao等[16]探索了参考光的不同幅度权重对相位误差率的影响，发现参考幅度达到信号的5倍，相位误差率开始随着参考权重的增加而逐渐增加。为了缩短迭代次数，降低相位误差率，Chen等提出了一种动态采样迭代相位检索方法。 Liu等[26]设计了一种基于压缩感知的高噪声容限解码方法，以减少噪声的影响，旨在减少相位误差。 纠错编码(ECC)是降低RBER和提高数据可靠性的有效方法。低密度奇偶校验码（Low Density Parity Check Code，LDPC）是一类具有稀疏校验矩阵的线性分组码，不仅有逼近Shannon限的良好性能，而且译码复杂度较低, 结构灵活，是近年信道编码领域的研究热点，目前已广泛应用于深空通信、光纤通信、卫星数字视频和音频广播等领域[19][27]。

目前的研究进展

本课题研究的相位型全息存储LDPC码优化方法，通过提高LDPC 译码纠错性能,不仅能够提升全息存储可靠性，而且对提升系统读性能具有重要意义。当系统中具有很高的RBER时，我们发现相邻的不同阶相位分布之间出现交叉重叠现象，如图2所示，这无疑给数据读取过程中的相位判决带来困难，因为处于交叉位置的相位可能属于左边相位，也可能属于右边相位，会导致较高的相位错误率（phase error rate, PER）.如果直接使用传统的LDPC码进行纠错，不仅会导致译码迭代次数的上升，甚至还会引起新的错误，如图3所示.这是因为当RBER超出LDPC码的纠错能力范围之后，即使达到最大的译码迭代次数，数据帧中的错误比特也不能被完全纠正过来.高的RBER意味着从全息信道向译码器发送的初始LLR信息的精度较低，导致LDPC译码性能下降.因此，研究如何获取高精度的初始LLR信息对提升相位型全息数据存储的可靠性十分关键.针对相位型同轴全息存储系统，本课题组提出了两种LDPC码优化方案，分别是相位分布感知的LDPC码优化方案（PDAL方案）[35]和参考光辅助的LDPC码优化方案[36]。

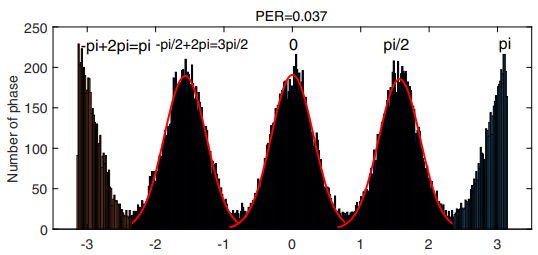
重建相位分布

图3（a）重建相位分布

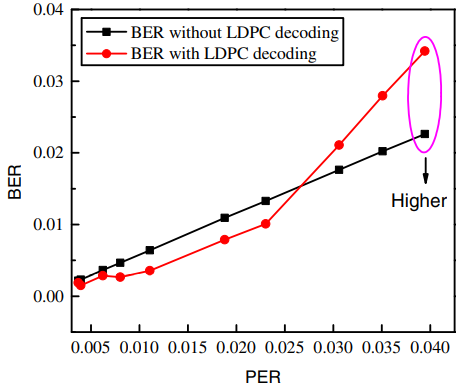
使用LDPC码前的BER示意图

图3（b）使用LDPC码前的BER示意图

相位分布感知的LDPC码优化方案

与硬判决相比，LDPC码的软判决译码算法能充分利用信道的信息.由于重建相位的分布受信道的影响，因此重建相位的分布信息能被用来优化LLR信息[26].在一个相位周期内，传统的硬判决方法是将相位状态的中间值作为参考相位，只有4个参考相位.为了区分重叠处的相位，PDAL方案设置了更细粒度的多个参考相位,如图4所示，一共施加了12个参考相位,以获取具有更高精度的LLR信息，从而提高LDPC码的译码性能.

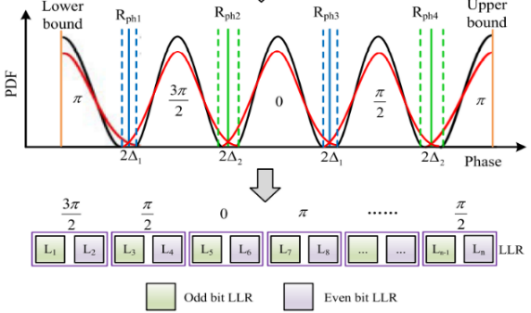
相位分布感知的LLR 优化方法示意图

图4 相位分布感知的LLR 优化方法示意图

实验验证了该方法的有效性.当PER为0.04时，与未利用相位分布的传统方法相比，PDAL方案使BER平均降低51.5%，译码迭代次数平均降低26.9%，译码失败率平均降低51.8%.在PER低于0.02时，两种方案的译码失败率差异很小.随着PER增加，PDAL方案的优越性愈加明显，这说明该方案显著提升了LDPC码的纠错能力和译码性能.并且，四组不同 的取值对译码性能的影响十分微小，这反应了该方法的灵活性和有效性.

参考光辅助的LDPC码优化

PDAL方案对初始LLR信息的优化需要依赖重建相位的分布.除此方法之外，该课题组还提出了一种参考光辅助的提升相位型同轴全息存储可靠性的方法.该方法利用参考光信息在记录和读取的过程中总是已知的，将参考光作为先验信息优化LDPC译码，提高LDPC码的译码性能和纠错能力，进而提升全息存储的可靠性.

在配置每个待纠正比特的LLR时，需要考虑极性和幅值.比特“1”的极性为“+”，比特“0”的极性为“-”，如图5所示.在比特极性正确的情况下，LLR的幅值越大，可信度越高.在LDPC译码时，由于参考光所携带的数据，以下称为参考比特，在记录和读取的过程中都是已知的，因此参考比特的可信度远高于未知的信息比特和校验比特.设定参考比特中的比特“0”的LLR为p， ；比特“1”的LLR为m，其中 保证了参考比特的LLR幅值大于信息比特和校验比特的幅值.通过放大参考比特的LLR幅值，提高了LLR信息的精度.

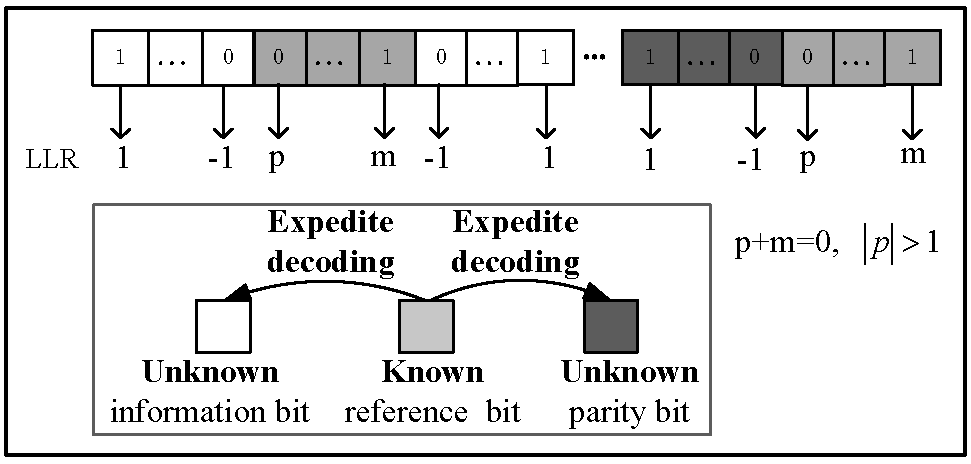
参考光辅助的LDPC译码方法中LLR配置示意图

图5 参考光辅助的LDPC译码方法中LLR配置示意图

实验验证了该方案的有效性.当PER为0.019时，与传统LDPC码相比，该方法可将比特错误率(BER)降低38.8%，不可校正误码率(UBER)降低24.9%，译码迭代时间减少29.9%，译码迭代次数减少14.8%，译码成功率提高约38.4%.图6展示了未利用纠错码、利用传统LDPC码以及参考光辅助的LDPC码纠错后的相位错误分布.如图6(a)展示的是未利用纠错码的原始相位错误率为0.025；如图6(b)所示，当传统LDPC码的译码迭代次数达到所设定的译码迭代次数最大值30时，相位错误率为0.019；如图6(c)所示,当利用参考光辅助的LDPC译码方案时，在译码迭代次数为20时，相位错误率为0.008；如图6(d)所示,在译码迭代次数为28时，相位错误率为0.与未利用参考光的传统LDPC码方案相比，参考光辅助的LDPC码优化方案显著降低了相位错误率和译码迭代次数，提高了相位型同轴全息存储系统的可靠性

利用IFT算法重建后的相位错误分布（PER=0.025）

(a)利用IFT算法重建后的相位错误分布（PER=0.025）

利用传统的LDPC码后的相位错误分布（译码迭代次数为30，PER=0.019）

(b)利用传统的LDPC码后的相位错误分布（译码迭代次数为30，PER=0.019）

利用参考光辅助的LDPC码后相位错误分布（译码迭代次数为20,PER=0.008）

(c)利用参考光辅助的LDPC码后相位错误分布（译码迭代次数为20,PER=0.008）

利用参考光辅助的LDPC码后相位错误分布（译码迭代次数为28，PER=0）

(d)利用参考光辅助的LDPC码后相位错误分布（译码迭代次数为28，PER=0）

图6 不同情况下的相位错误分布图

结 论

大数据时代，高密度大容量的存储需求与日剧增.全息存储技术凭借存储密度高、数据转换速率快以及节能安全等优势极有可能成为新一代存储技术的主角.本文从全息存储技术出发，着重介绍了全息存储系统中的纠错码研究现状，特别是面向相位型同轴全息存储系统的LDPC码优化方案，分别是相位分布感知的LDPC码优化方案以及参考光辅助的LDPC译码方案.但是，由于全息存储系统中噪声的复杂性以及相位重建算法的局限性，提高数据保存可靠性仍是需要重点关注和研究的问题，也是决定相位型同轴全息存储器实现商品化的关键.提高可靠性的方式不只是纠错码，还有数据编解码、调制以及噪声抑制等技术，更为丰富和完善的理论研究势必将相位型同轴全息存储推向更为广阔的舞台.

主要参考文献

  • [1] DataAge2025. https://www.seagate.com/files/www-content/our-story/trends/files/idc-seagate-dataage-whitepaper.pdf.
  • [2] 谭小地. 大数据时代的光存储技术[J]. 红外与激光工程, 2016, 45(9):4.
  • [3] Kumar S, McCaffrey T R. Engineering economics at a hard disk drivemanufacturer [J]. Technovation, 2003, 23 (2): 749- 755.
  • [4] Okazaki Y, Hara K, Kawashima T, et al. Estimating the archival life of metal particulate tape [J]. Magnetics IEEE Transactions on, 1992, 28(5): 2365-2367.
  • [5] Sony Corporation, Professional Solutions Group. Optical Disc Archive White Paper vI.IO [M]. Japan: Sony Corporation, 2013.
  • [6] J. F. Heanue, M. C. Bashaw, and L. Hesselink, “Volume Holographic Storage and Retrieval of Digital Data,” Science 265(5173), 749–752 (1994).
  • [7] H. J. Coufal, D. Psaltis, and G. T. Sincerbox, eds., Holographic Data Storage (Springer-Verlag, 2000).
  • [8] L. Dhar, K. Curtis, M. Tackitt, M. Schilling, S. Campbell, W. Wilson, A. Hill, C. Boyd, N. Levinos, and A. Harris, “Holographic storage of multiple high-capacity digital data pages in thick photopolymer systems,” Opt. Lett. 23(21), 1710–1712 (1998).
  • [9] S. S. Orlov, W. Phillips, E. Bjornson, Y. Takashima, P. Sundaram, L. Hesselink, R. Okas, D. Kwan, and R. Snyder, “High-transfer-rate high-capacity holographic disk data-storage system,” Appl. Opt. 43(25), 4902–4914 (2004).
  • [10] H. Horimai and X. Tan, “Advanced collinear holography,” Opt. Rev. 12(2), 90–92 (2005).
  • [11] X. Tan, O. Matoba, T. Shimura, and K. Kuroda, “Improvement in holographic storage capacity by use of double-random phase encryption,” Appl. Opt. 40(26), 4721–4727 (2001).
  • [12] T. Nobukawa and T. Nomura, “Correlation-Based Multiplexing of Complex Amplitude Data Pages in a Holographic Storage System Using Digital Holographic Techniques,” Polymers 9(12), 375 (2017).
  • [13] T. Nobukawa and T. Nomura, “Linear phase encoding for holographic data storage with a single phase-only spatial light modulator,” Appl. Opt. 55(10), 2565–2573 (2016).
  • [14] H. Horimai and X. Tan, “Holographic information storage system: today and future,” IEEE Trans. Magn. 43, 943–947 (2007).
  • [15] X. Lin, J. Hao, K. Wang, Y. Zhang, H. Li, and X. Tan, “Frequency expanded non-interferometric phase retrieval for holographic data storage,” Opt. Express 28, 511–518 (2020).
  • [16]J. Hao, K. Wang, Y. Zhang, H. Li, X. Lin, Z. Huang, and X. Tan, “Collinear non-interferometric phase retrieval for holographic data storage,” Opt. Express 28, 25795–25805 (2020).
  • [17] Y. Yu, Y. Chen, K. Huang, C. Cheng, T. Yang, S. Lin, and C. Sun, “Reduction of phase error on phase-only volume-holographic disc rotation with pre-processing by phase integral,” Opt. Express 28, 28573–28583 (2020).
  • [18] N. Ishii, Y. Katano, T. Muroi, and N. Kinoshita, “Spatially coupled low-density parity-check error correction for holographic data storage,”Japanese Journal of Applied Physics 56, 09NA03 (2017).
  • [19] J. Kim and J. Lee, “Two-dimensional SOVA and LDPC codes for holographic data storage system,”IEEE Transactions on Magnetics, 45 (5), 2260-2263 (2009).
  • [20] R. Gallager, “Low-density parity-check codes,”IRE Transactions on information theory.
  • [21] Yeh-Wei Yu, Yuan-Cheng Chen, Kun-Hao Huang, Chih-Yuan Cheng, Tsung-Hsun Yang, Shiuan-Huei Lin, and Ching-Cherng Sun, “Reduction of phase error on phase-only volume-holographic disc rotation with pre-processing by phase integral,” Opt. Express 28, 28573-28583 (2020).
  • [22] Zhao Y, Wu F, Lin X, et al. Phase-distribution-aware adaptive decision scheme to improve the reliability of holographic data storage[J]. Optics Express, 2022, 30(10): 16655-16668.
  • [23]Xu K, Huang Y, Lin X, et al. Unequally spaced four levels phase encoding in holographic data storage[J]. Optical Review, 2016, 23(6): 1004-1009.
  • [24] X. Lin, Y. Huang, T. Shimura, R. Fujimura, Y. Tanaka, M. Endo, H. Nishimoto, J. Liu, Y. Li, Y. Liu, and X. Tan, “Fast non-interferometric iterative phase retrieval for holographic data storage,” Opt. Express 25, 30905–30915 (2017).
  • [25] Chen R, Hao J, Yu C, et al. Dynamic sampling iterative phase retrieval for holographic data storage[J]. Optics Express, 2021, 29(5): 6726-6736.
  • [26] J. Liu, L. Zhang, A. Wu, Y. Tanaka, S. Shigaki, T. Shimura, X. Lin, and X. Tan, “High noise margin decoding of holographic data page based on compressed sensing,” Opt. Express 28, 7139–7151 (2020).
  • [27] F. Wu, M. Zhang, Y. Du, W. Liu, Z. Lu, J. Wan, Z. Tan, and C. Xie, “Using error modes aware LDPC to improve decoding performance for 3-D TLC NAND flash,” IEEE Transactions on Computer Aided Design of Integrated Circuits and Systems 39(4), 909-921 (2020).
  • [28] J. Hao, X. Lin, Y. Lin, H. Song, R. Chen, M. Chen, K. Wang, and X. Tan, “Lensless phase retrieval based on deep learning used in holographic data storage,” Opt. Lett. 46, 4168–4171 (2021).
  • [29] Q. Yu, M. Zhang, Y. Zhao, F. Wu, and C. Xie, “Exploiting LDPC coding to improve data reliability for phase modulated holographic storage,” Proc. SPIE 12066, 1206619 (2021).
  • [30] F. Wu, M. Zhang, Y. Du, X. He, P. Huang, C. Xie, and J. Wan, “A program interference error aware LDPC scheme for improving NAND flash decoding performance,” ACM Trans. Embedded Comput. Syst. 16, 141 (2017).
  • [31] J. Zhao, F. Zarkeshvari, and A. H. Banihashemi, “On implementation of min-sum algorithm and its modifications for decoding low-density parity-check (LDPC) codes,” IEEE Trans. Commun. 53, 549–554 (2005).
  • [32] C. Gu, F. Dai, and J. Hong, “Statistics of both optical and electrical noise in digital volume holographic data storage,” Electron. Lett. 32, 1400–1402 (1996).
  • [33] C. Gu, G. Sornat, and J. Hong, “Bit-error rate and statistics of complex amplitude noise in holographic data storage,” Opt. Lett. 21, 1700–1702 (1996).
  • [34] M. Tokoro and R. Fujimura, “Single-shot detection of four-level phase modulated signals using inter-pixel crosstalk for holographic data storage,” Jpn. J. Appl. Phys. 60, 022004 (2021).
  • [35] Q. Yu, F. Wu, M. Zhang, et al. Improving reliability using phase distribution aware LDPC code for holographic data storage[J]. Applied Opt.2022,61(21):6119-6127.
  • [36] Q. Yu, F. Wu, M. Zhang, et al. Fast phase error correction with reference beam-assisted LDPC coding for collinear holographic data storage[J]. Optics Express, 2023,31(12):20345-20363.